In den letzten Wochen ist dem ein oder anderen vielleicht mein Interesse für mathematische Fragestellungen aufgefallen, das durch das Jahr der Mathematik geweckt wurde. In den letzten Tagen habe ich mich nun mit einem interessanten Phänomen beschäftigt, welches die Mathematiker anscheinend zum Verzweifeln bringt.
Ausgangspunkt ist die schönste aller Primzahlen, die 2 (denn nur sie ist gerade). Alle anderen geraden Zahlen sind keine Primzahlen, sie sind Vielfache der 2.
Primzahlen haben was mit Multiplizieren zu tun. Sie zeichnen sich dadurch aus, dass sie nicht durch Multiplikation „erreichbar“ sind. Es gibt keine Möglichkeit, sie als Produkt vieler anderer ganzzahliger Zahlen darzustellen.
Doch wie sieht das mit dem Addieren aus? Wenn man zwei Primzahlen >2 addiert, kommt eine gerade Zahl heraus. 7+3=10; 23+7=30 und so weiter… (Auf eine vollständige Aufzählung sei hier verzichtet: Primzahlen >2 sind immer ungerade, und die Summe zweier ungerader Zahlen ist immer gerade).
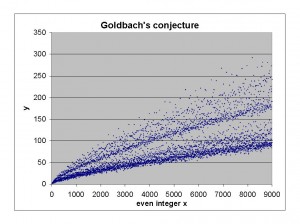
Und nun kommt Herr Goldbach ins Spiel. Er sprach die Vermutung aus, das jede gerade Zahl >3 auf mindestens eine Art als Summe zweier Primzahlen darzustellen ist. Für einen Ingenieur ist das Nachvollziehbar: 4=2+2; 6=3+3; 8=5+3; 10=7+3 oder 10=5+5; 12=7+5… Das kann man natürlich ins Extrem treiben: Folgende Grafik (geklaut bei Wikipedia) zeigt auf der X-Achse die geraden Zahlen von 2 bis 9000 und auf der y-Achse die Anzahl der möglichen Schreibweisen als Summe zweier Primzahlen.
Goldbach selbst hat die Vermutung noch nicht so scharf formuliert, er wollte die Summe von 3 Primzahlen auch als gültig zählen lassen. Doch stürzt sich die Mathematiker nach wie vor auf die scharfe Formulierung. Goldbachs Vermutung zu widerlegen oder zu bestätigen, würde einen Platz in der Ahnensammlung der großen Köpfe der Mathematik einbringen.
Auffällig sind in der Grafik (wenn man das Streuen als Rauschen betrachtet), dass die Anzahl der möglichen Summen einen ansteigende Tendenz hat. Ein schließender Statistiker würde also messerscharf schließen, dass in der vorliegenden Sichprobe ein Trend zu entdecken sei. Manche Statistiker finden sogar zwei Trends.
Doch reicht so ein einfacher statistisch belegbarer Trend nun beim besten Willen nicht aus, um zu begründen, dass nicht doch mal eine gerade Zahl nicht als Summe zweier Primzahlen dargestellt werden kann.